数字控制开关电源

开关电源数字控制

相关参考链接

B战杨帅哥的开关电源数字控制

知乎开关频率与闭环带宽

1 数字控制开关电源的重要内容

1	采样时间点对滞后的影响（零阶保持器），ADC采样点与相位优化的关系
2	控制带宽频率与开关频率的关系（为什么是五倍的关系)
3	s平面与z平面的映射关系
4	使用梯形积分法将s域传递函数变为z域传递函数，之后差分化变为代码。在Z域下直接设计补偿控制器。
5	Z变换到代码中的具体操作
6	MATLAB的sisotool工具、c2d工具等使用

2 采样时间点对滞后的影响（零阶保持器），ADC采样点与相位优化的关系

$$图1$$

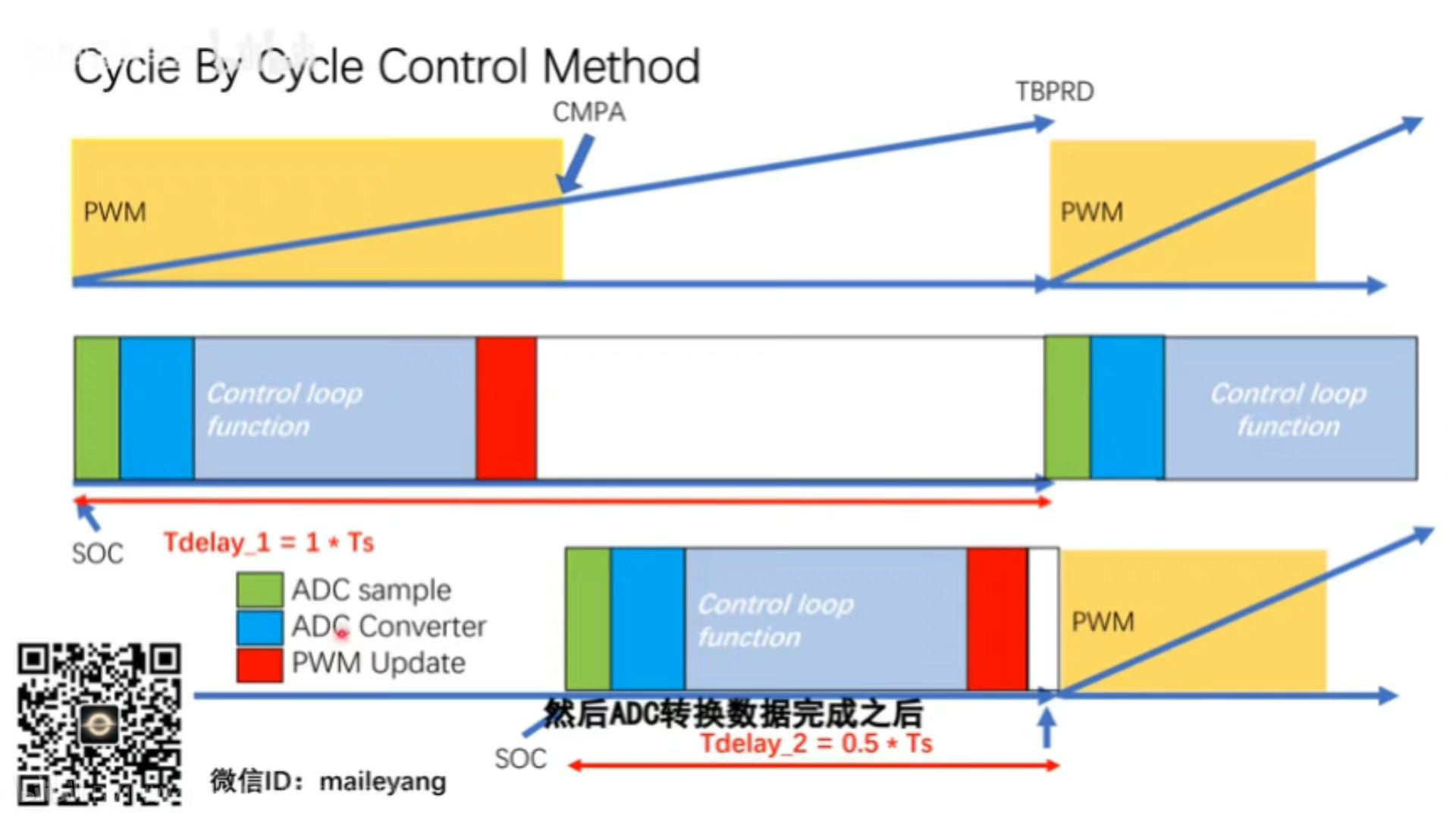
计算$fx$频率下的相位余量公式为：

$$\bigtriangleup \phi =-360^{\circ } \times \frac{fx }{Fx} \times Kd$$

$Fx$为采样频率	$Kd$为延迟周期比例

在$Fs=100KHz$与$fx=20kHz$的情况下计算。

在PWM周期开始采样，$Kd=1$,计算相位在20KHz滞后$72^{o}$。

在PWM周期一般开始采样，Kd=0.5，计算相位在20KHz滞后$36^{o}$。

应该尽可能的在PWM周期中后段触发ADC采样，可以有利于系统稳定性，提高相位余量。

数字控制的延时问题

就是如果采样频率等于开关频率，在环路中会引入$540^{o}$的相位滞后，也就是说，在开关频率处会引入540度的相位滞后！即使截止频率是开关频率的$\frac{1}{10} $，光是数字控制在截止频率处也会引入54度的相位滞后，其实也很难补偿回来了。所以说，在数字控制下，为了保持控制系统有足够的相角裕度，其截止频率会更低一些，从而减小数字控制引入的相角滞后的影响。当然还有一种办法是提高采样频率，现在我们做逆变器一般采样频率是开关频率的两倍。这也是为了减小数字控制造成的延迟。

3 控制带宽频率与开关频率的关系（为什么是五倍的关系)

$$图2$$

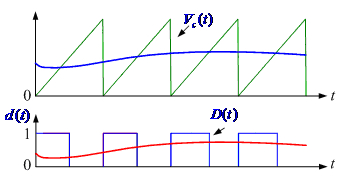
​ 假设一个电力电子变换器开关频率为100k，调制波频率为10k，那么经过PWM环节得到占空比，状态空间平均法认为得到的占空比也是一个10k的交流信号(如图2所示的红线)，即PWM环节等效为一个比例环节。但实际上不完全是这样的，对占空比做傅里叶分析，可以知道占空比中除了10k的分量外，还有90K，110K，190K……的分量，那么状态空间平均法的准确度就依赖于这些非基波分量的抑制程度，显然，带宽越低，对这些非基波频率的分量抑制能力越强，状态空间平均法得到的模型就越准确。这是电力电子变换器环路截止频率为开关频率的1/5~1/10的重要原因之一，当环路截止频率超过开关频率的1/5以后，用状态空间平均法得出的模型就和实际模型差距比较大了。

4 s域和z域的映射关系

基础知识部分

首先对于是一个负反馈来说。极点必须位于s平面的左半平面的原因是：对于负反馈系统的话，假设分母为$(s+p1) (s+p2)$可知极点为$p1 p2$的,经过拉式反变换。

最后变换出的输出量中有含有乘法$e^{-pt}$，此时只有p满足在S左半平面，当$t\to\infty $时有$e^{-pt}\to0$,此时系统误差可趋向于0，因此系统稳定。

首先B站视频图像化展示s域z域的关系

$$视频1 拉式变换 S域到Z平面$$ $$图3$$

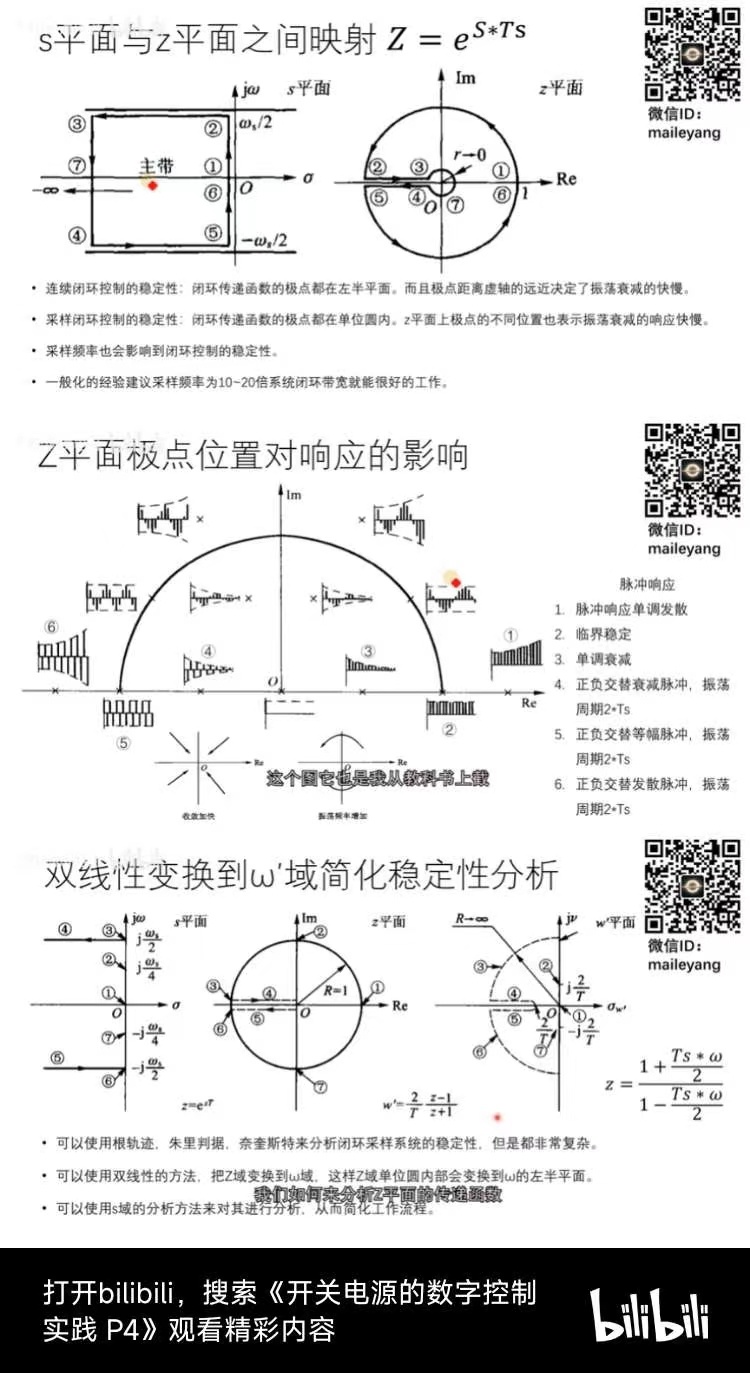
5 z变换实操案例

基础知识1 z变换

序列$x(n)$的z变换为$X(z)$,序列$y(n)=x(n-1)$的z变换为$Y(z)$

$$Y\left ( z \right )=\sum_{n=-\infty }^{\infty} y(n)z^{-n}=\sum_{n=-\infty }^{\infty} x(n-1)z^{-n}$$

$K=n-1$代入变为

$$Y\left ( z \right )=\sum_{n=-\infty }^{\infty} x(k)z^{-(k+1)}=\sum_{n=-\infty }^{\infty} x(k)z^{-k}z^{-1}$$

经整理得

$$Y\left ( z \right )=z^{-1}\sum_{n=-\infty }^{\infty} x(k)z^{-k}=z^{-1}[X(z)]$$

可以如下图进行展示

$$图4$$

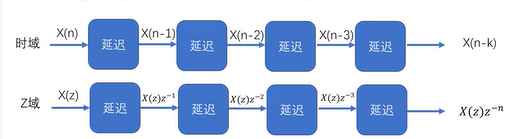
基础知识2 梯形积分法的Z变换相关公式

$$s=\frac{2}{T}\frac{(z-1)}{z+1}=\frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}}\\T为采样周期$$

计算实例

步骤1获取目标同步函数

$$H_{c} (s)=\frac{w_{P0}}{s}\frac{(\frac{s}{w_{Z1}}+1 )(\frac{s}{w_{Z2}}+1 )} {(\frac{s}{w_{P1}}+1 )(\frac{s}{w_{P2}}+1 )} \\s=\frac{2}{T_{s}}\frac{(z-1)}{z+1}=\frac{2}{T_{s}}\frac{1-z^{-1}}{1+z^{-1}} \\$$

将s代入

$$H (\frac{2(1-\frac{1}{z} )}{T(\frac{1}{z}+1 )} )=\frac{Tw_{P0} (\frac{2(1-\frac{1}{z} )}{T_{w_{Z1}}(\frac{1}{z}+1)}+1) (\frac{2(1-\frac{1}{z} )}{T_{w_{Z2}}(\frac{1}{z}+1)}+1) (\frac{1}{z}+1 )} {(\frac{2(1-\frac{1}{z} )}{T_{w_{P1}}(\frac{1}{z}+1)}+1) (\frac{2(1-\frac{1}{z} )}{T_{w_{P2}}(\frac{1}{z}+1)}+1) (1-\frac{1}{z} )}$$

进行因式分解

$$\begin{equation} \begin{aligned} H_{C}[z]&=\frac{ \begin{equation} \begin{aligned} & w_{P0}w_{P1}w_{p2}((T^{3}w_{Z1}+2T^{2})w_{Z2}+2T^{2}w_{Z1}+4T)z^{3}+ \\ & w_{P0}w_{P1}w_{p2}((3T^{3}w_{Z1}+2T^{2})w_{Z2}+2T^{2}w_{Z1}-4T)z^{2}+\\ & w_{P0}w_{P1}w_{p2}((3T^{3}w_{Z1}-2T^{2})w_{Z2}-2T^{2}w_{Z1}-4T)z^{1}+\\ & w_{P0}w_{P1}w_{p2}((T^{3}w_{Z1}-2T^{2})w_{Z2}-2T^{2}w_{Z1}+4T)z^{0} \end{aligned} \end{equation} }{ \begin{equation} \begin{aligned} & w_{Z1}w_{Z2}((2T^{2}w_{P1}+4T)w_{P2}+2T w_{P1}+8)z^{3}+ \\ & w_{Z1}w_{Z2}((2T^{2}w_{P1}-4T)w_{P2}-2T w_{P1}-24)z^{2}+ \\ & w_{Z1}w_{Z2}((-2T^{2}w_{P1}-4T)w_{P2}-2T w_{P1}+24)z^{1}+\\ & w_{Z1}w_{Z2}((-2T^{2}w_{P1}+4T)w_{P2}-2T w_{P1}-24)z^{0} \end{aligned} \end{equation} } \\ &=\frac{B_{3}z^{-3}+B_{2}z^{-2}+B_{1}z^{-1}+B_{0}} {-A_{3}z^{-3}-A_{2}z^{-2}-A_{1}z^{-1}+1} \end{aligned} \end{equation}$$

上下同时乘$z^{-3}$即为时间向前移动3个延时

$$\begin{equation} \begin{aligned} H_{C}[z]&=\frac{ \begin{equation} \begin{aligned} & B_{0}\to w_{P0}w_{P1}w_{p2}((T^{3}w_{Z1}+2T^{2})w_{Z2}+2T^{2}w_{Z1}+4T)z^{0}+ \\ & B_{1}\to w_{P0}w_{P1}w_{p2}((3T^{3}w_{Z1}+2T^{2})w_{Z2}+2T^{2}w_{Z1}-4T)z^{-1}+\\ & B_{2}\to w_{P0}w_{P1}w_{p2}((3T^{3}w_{Z1}-2T^{2})w_{Z2}-2T^{2}w_{Z1}-4T)z^{-2}+\\ & B_{3}\to w_{P0}w_{P1}w_{p2}((T^{3}w_{Z1}-2T^{2})w_{Z2}-2T^{2}w_{Z1}+4T)z^{-3} \end{aligned} \end{equation} }{ \begin{equation} \begin{aligned} & A_{0}\to w_{Z1}w_{Z2}((2T^{2}w_{P1}+4T)w_{P2}+2T w_{P1}+8)z^{0}+ \\ & A_{1}\to w_{Z1}w_{Z2}((2T^{2}w_{P1}-4T)w_{P2}-2T w_{P1}-24)z^{-1}+ \\ & A_{2}\to w_{Z1}w_{Z2}((-2T^{2}w_{P1}-4T)w_{P2}-2T w_{P1}+24)z^{-2}+\\ & A_{3}\to w_{Z1}w_{Z2}((-2T^{2}w_{P1}+4T)w_{P2}-2T w_{P1}-24)z^{-3} \end{aligned} \end{equation} } \\ \end{aligned} \end{equation}$$

步骤2归一化

归一化的目的为使得$A_{0}=1$，将$H_{Z}[z]$上线同乘$\frac{1}{w_{Z1}w_{Z2}((2T^{2}w_{P1}+4T)w_{P2}+2T w_{P1}+8)}$然后就可以得到下式：

$$\begin{equation} \begin{aligned} H_{C}[z]&=\frac{ \begin{equation} \begin{aligned} & B_{0}\to \frac{w_{P0}w_{P1}w_{p2}((T^{3}w_{Z1}+2T^{2})w_{Z2}+2T^{2}w_{Z1}+4T)z^{0}}{w_{Z1}w_{Z2}((2T^{2}w_{P1}+4T)w_{P2}+2T w_{P1}+8)}+ \\ & B_{1}\to \frac{w_{P0}w_{P1}w_{p2}((3T^{3}w_{Z1}+2T^{2})w_{Z2}+2T^{2}w_{Z1}-4T)z^{-1}}{w_{Z1}w_{Z2}((2T^{2}w_{P1}+4T)w_{P2}+2T w_{P1}+8)}+\\ & B_{2}\to \frac{w_{P0}w_{P1}w_{p2}((3T^{3}w_{Z1}-2T^{2})w_{Z2}-2T^{2}w_{Z1}-4T)z^{-2}}{w_{Z1}w_{Z2}((2T^{2}w_{P1}+4T)w_{P2}+2T w_{P1}+8)}+\\ & B_{3}\to \frac{w_{P0}w_{P1}w_{p2}((T^{3}w_{Z1}-2T^{2})w_{Z2}-2T^{2}w_{Z1}+4T)z^{-3}}{w_{Z1}w_{Z2}((2T^{2}w_{P1}+4T)w_{P2}+2T w_{P1}+8)} \end{aligned} \end{equation} }{ \begin{equation} \begin{aligned} & A_{0}\to 1+ \\ & A_{1}\to \frac{w_{Z1}w_{Z2}((2T^{2}w_{P1}-4T)w_{P2}-2T w_{P1}-24)z^{-1}}{w_{Z1}w_{Z2}((2T^{2}w_{P1}+4T)w_{P2}+2T w_{P1}+8)}+ \\ & A_{2}\to \frac{w_{Z1}w_{Z2}((-2T^{2}w_{P1}-4T)w_{P2}-2T w_{P1}+24)z^{-2}}{w_{Z1}w_{Z2}((2T^{2}w_{P1}+4T)w_{P2}+2T w_{P1}+8)}+\\ & A_{3}\to \frac{w_{Z1}w_{Z2}((-2T^{2}w_{P1}+4T)w_{P2}-2T w_{P1}-24)z^{-3}}{w_{Z1}w_{Z2}((2T^{2}w_{P1}+4T)w_{P2}+2T w_{P1}+8)} \end{aligned} \end{equation} } \\ \end{aligned} \end{equation}$$

步骤3 最终结果

$$H_{C}[z]=\frac{B_{3}z^{-3}+B_{2}z^{-2}+B_{1}z^{-1}+B_{0}} {-A_{3}z^{-3}-A_{2}z^{-2}-A_{1}z^{-1}+1}\\\\\\ \begin{equation} \begin{aligned} B_{0}= &\frac{w_{P0}w_{P1}w_{p2}((T^{3}w_{Z1}+2T^{2})w_{Z2}+2T^{2}w_{Z1}+4T)z^{0}}{w_{Z1}w_{Z2}((2T^{2}w_{P1}+4T)w_{P2}+2T w_{P1}+8)} \\ B_{1}=&\frac{w_{P0}w_{P1}w_{p2}((3T^{3}w_{Z1}+2T^{2})w_{Z2}+2T^{2}w_{Z1}-4T)z^{-1}}{w_{Z1}w_{Z2}((2T^{2}w_{P1}+4T)w_{P2}+2T w_{P1}+8)}\\ B_{2}= &\frac{w_{P0}w_{P1}w_{p2}((3T^{3}w_{Z1}-2T^{2})w_{Z2}-2T^{2}w_{Z1}-4T)z^{-2}}{w_{Z1}w_{Z2}((2T^{2}w_{P1}+4T)w_{P2}+2T w_{P1}+8)}\\ B_{3}= &\frac{w_{P0}w_{P1}w_{p2}((T^{3}w_{Z1}-2T^{2})w_{Z2}-2T^{2}w_{Z1}+4T)z^{-3}}{w_{Z1}w_{Z2}((2T^{2}w_{P1}+4T)w_{P2}+2T w_{P1}+8)} \\ \\ A_{1}= &\frac{w_{Z1}w_{Z2}((2T^{2}w_{P1}-4T)w_{P2}-2T w_{P1}-24)z^{-1}}{w_{Z1}w_{Z2}((2T^{2}w_{P1}+4T)w_{P2}+2T w_{P1}+8)} \\ A_{2}= &\frac{w_{Z1}w_{Z2}((-2T^{2}w_{P1}-4T)w_{P2}-2T w_{P1}+24)z^{-2}}{w_{Z1}w_{Z2}((2T^{2}w_{P1}+4T)w_{P2}+2T w_{P1}+8)}\\ A_{3}= &\frac{w_{Z1}w_{Z2}((-2T^{2}w_{P1}+4T)w_{P2}-2T w_{P1}-24)z^{-3}}{w_{Z1}w_{Z2}((2T^{2}w_{P1}+4T)w_{P2}+2T w_{P1}+8)} \end{aligned} \end{equation}$$

由上面可知手动离散化的过程是痛苦漫长的，但是可以用MATLAB中的

matlab为连续系统提供了离散化模型。利用$c2d()$函数可实现连续函数的快速离散化。$c2d()$函数的调研格式为：

$$\begin{equation} \begin{aligned} sysd &=c2d(sys,Ts)\\ sysd&=c2d(sys,Ts,method) \end{aligned} \end{equation}$$

式中，$sysd$为采样时间$Ts$的离散时间模型；输入参量$sys$为连续时间模型对象；$Ts$为采样周期。$Method$用来指定离散化采用的方法：

$zoh$	采用零阶保持器法，零阶保持器的作用是在信号传递过程中，把第nT时刻的采样信号值一直保持到第(n+1)T时刻的前一瞬时，把第(n+1)T时刻的采样值一直保持到(n+2)T时刻，依次类推，从而把一个脉冲序列变成一个连续的阶梯信号。因为在每一个采样区间内连续的阶梯信号的值均为常值，亦即其一阶导数为零，故称为零阶保持器；
$foh$	采用一阶保持器法，与上面不同的是，在信号传递过程中，两个相邻采样点之间的信号是一阶函数，起点和终点的值分别等于前后两个采样点的值则
$tustin$	采用双线性变换法
$prewarp$	采用改进的双线性变换法
$matched$	采用零极点匹配法

默认为$zoh$。

基$MATLAB$的的例子：求下式的$Z$变换：

$$G(s)=\frac{10(s+1)}{(s+3)(s+5)(s+7)}$$

步骤4 差分化

已知

$$\frac{y[z]}{x[z]}=\frac{B_{3}z^{-3}+B_{2}z^{-2}+B_{1}z^{-1}+B_{0}} {-A_{3}z^{-3}-A_{2}z^{-2}-A_{1}z^{-1}+1}$$

经化解可得

$$\begin{equation} \begin{aligned} {x[z]}\times (B_{3}z^{-3}+B_{2}z^{-2}+B_{1}z^{-1}+B_{0}) &= y[z]\times (-A_{3}z^{-3}-A_{2}z^{-2}-A_{1}z^{-1}+1) \\ B_{3}x_{n-3}+B_{2}x_{n-2}+B_{1}x_{n-1}+B_{0}x_{n} &= -A_{3}y_{n-3}-A_{2}y_{n-2}-A_{1}y_{n-1}+y_{n} \end{aligned} \end{equation}$$

可得最终差分化所得的差分方程：运行在处理器中

y是控制量 x是误差 下标为多少周期前

$$y_{n} = B_{3}x_{n-3}+B_{2}x_{n-2}+B_{1}x_{n-1}+B_{0}x_{n}+A_{3}y_{n-3}+A_{2}y_{n-2}+A_{1}y_{n-1}$$