1:自我介绍
| 姓名 | 牛淼 | 出生日期 | 1995-12-14 |
|---|---|---|---|
| 学历背景 毕业时间 |
本科:大连海事大学 硕士:大连海事大学 本硕连读:2021年7月份硕士毕业 |
民族 | 汉族 |
| 期望岗位 | 硬件工程师 嵌入式工程师 |
照片 |  |
2:能力列表
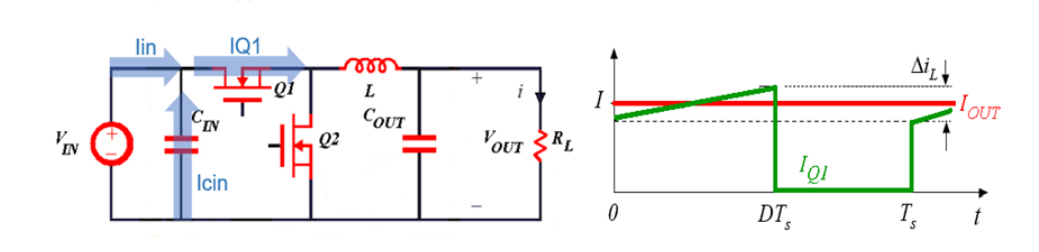
| 1:硬件部分 | 硬件1: 40kw 高压充电机(功率部分)设计,器件选型例如SIC模块选型、驱动模块等 ,测试方案设计,防雷,防浪涌设计等安规保护设计。 硬件2:船舶储能双向DC/DC变换器的硬件设计,buck-boost主电路PCB设计、采样驱动模块、STM系列主控板设计 |
|---|---|
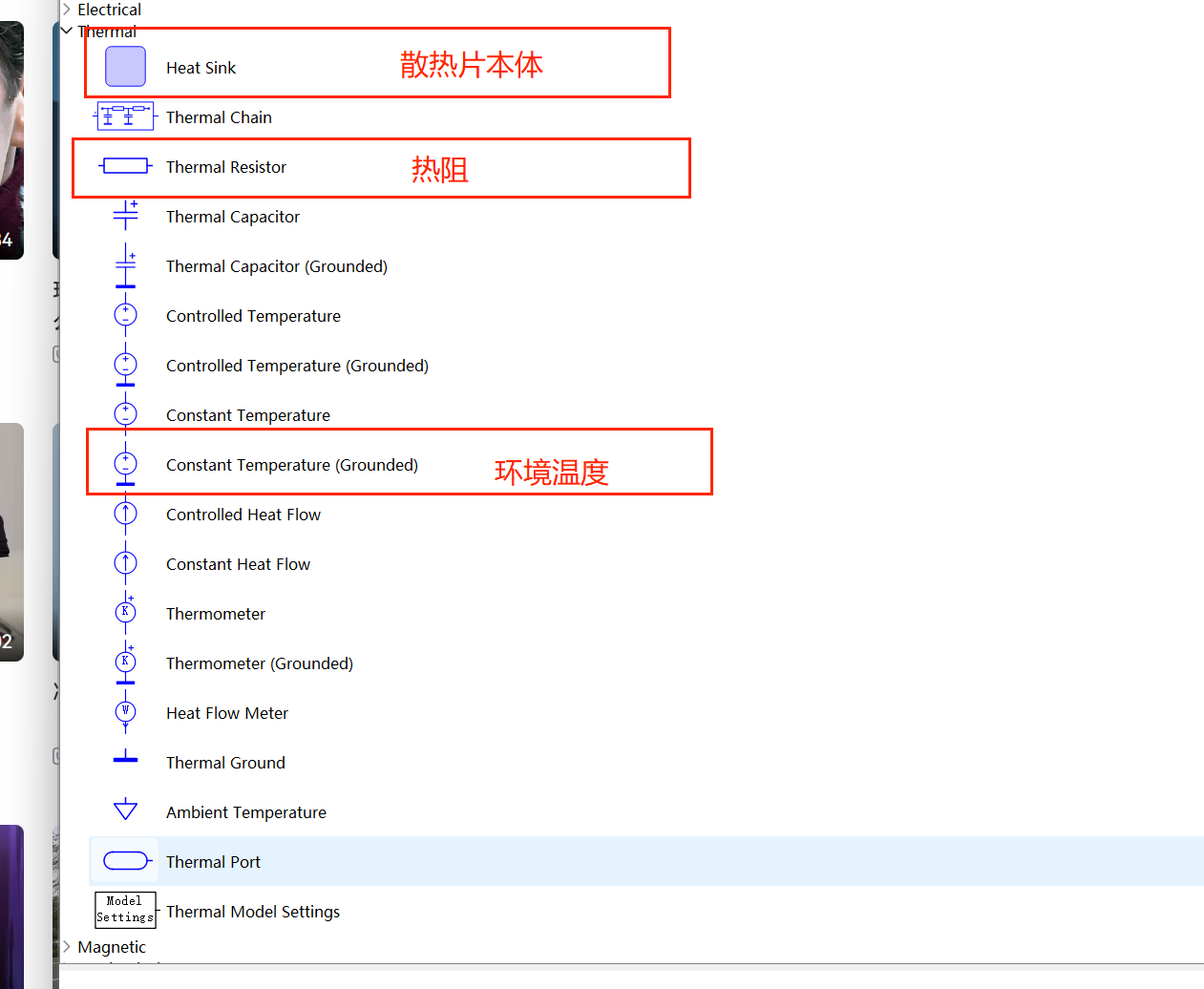
| 2 :硬件仿真部分 | 熟悉了解 $ANSYS SIwave $仿真:用于 $pdn$ 分析与大电流仿真(AD中的PDN插件也有相同功能); filterSolution 设计软件:用于滤波器设计; MATLAB 仿真:用于控制算法仿真,例如buck-boost变换器的控制测量仿真; simtrix辅助软件:掌握程度为了解或简单熟悉,用于搭建主拓扑电路用于波形仿真 LTspice软件:比较熟,简易方便用的多。AC分析,出伯德图; |
| 3 软件部分 | 已有成果:一个相关电力系统仿真平台软件,一个 Linux 下的纯后端软件,一个开关电源数字控制软件; 特种电力系统应用背景下,Linux(Ubuntu18.04)环境下的 QT 架构电力系统控制软件开发: 所知识点有QT的重绘事件,信号与槽,数据结构,指针; 电力力系统节点计算机程序开发(petalinux 环境)、私有 CAN 通信协议搭建:所涉及知识点有指针、链表、责任链模式开发、shell脚本编写,使用python配置数据库点表; 开关电源主控模块的软件开发,包括MT1640、电压电流双闭环控制、LVGL的GUI应用开发、安全保护设置,定时中断任务。 其他软件工作,基于传递函数设计在 DSP 中所运行的差分公式,即实际运行代码; 主力语言: c++; |
| 4 自学与抗压 | 有较强的自学能力,CSDN个人主页:阿水的CSDN主页,其中《自抗扰控制入门之ESO篇》系列数篇原创博文为CSDN原力计划推荐博客,单文章阅读量2W,总阅读量9W; |
| 5 经验时长 | 嵌入式(四年),电源PCB设计(四年),硬件电路调试(三年半),Linux开发(一年),摄影后期(四年) |
| 6 文档能力 | 可熟读英文相关文献,良好的文档编写习惯; |