1：boost电感计算（两电平）

本文是个人的学习记录，多学原视频大佬的分析：

1	最小输入电压为12V，故以此设计电感
2	由$V_{out}=\frac{V_{in} }{1-D}$。可知，D=0.8 80%
3	开关周期为$\frac{1}{T}$可得，周期$10\mu s$
4	开关管导通时间为$8 \mu s$
5	电压秒平衡$V_{in}\times t_{on}=12V\times 8\mu s=96 V \mu s$
6	根据$r=\frac{V\bigtriangleup t}{L\times I_{avg} } $和$ I_{avg}=\frac{I_{o} }{1-D} $可得 “r是纹波率 $I_{avg}$平均电流 ” 可得“$r= 0.4=\frac{12V\times 8\mu s }{L\times10 } \to 4=\frac{96 V \mu s}{L} \to L=24\mu H$”
7	最大电流为10A+4A =14A
8	确定电感 14A $24 \mu H$

2：三电平工作原理

图1

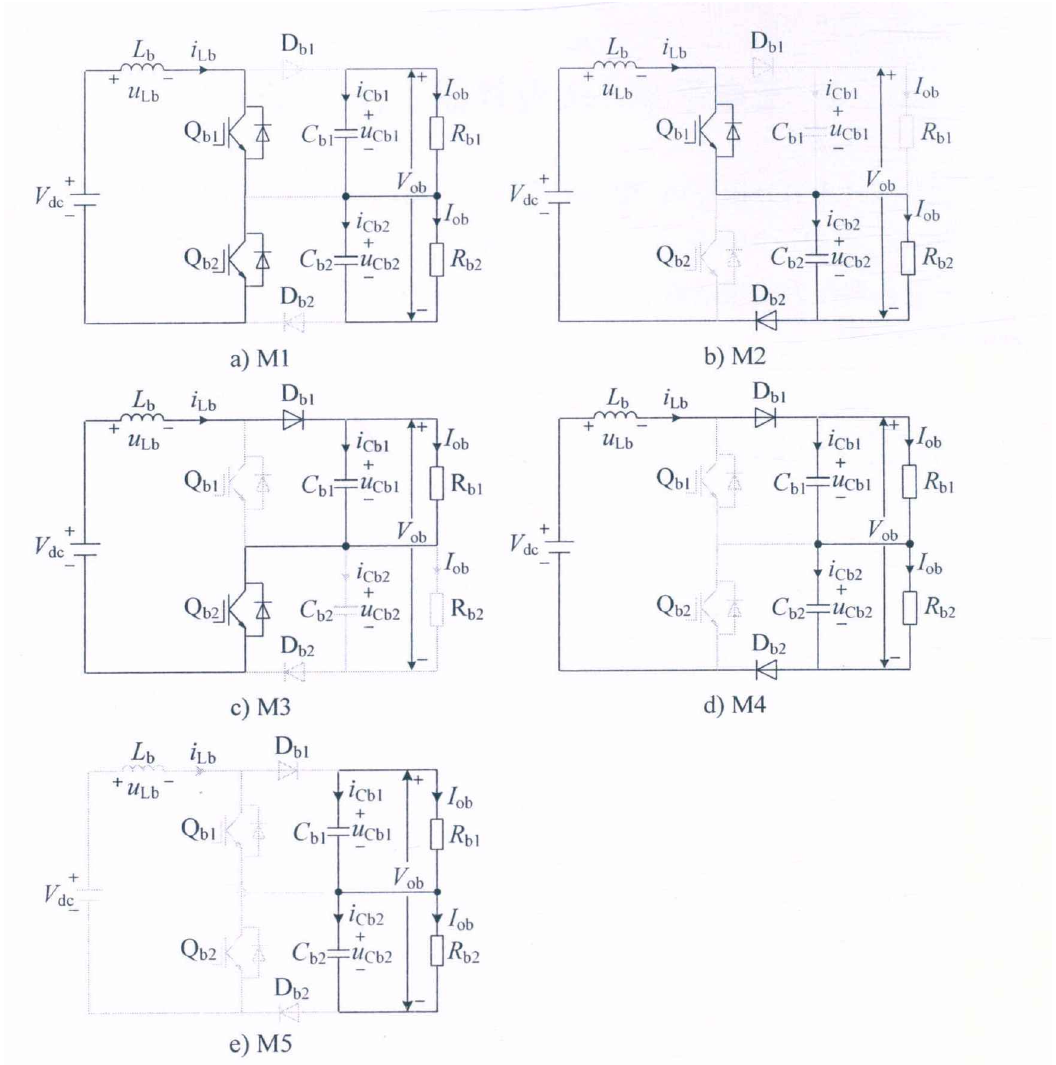
工作模式的区别:根据占空比大小而有区别。

$D_{on} \le 50 $	$M2\longrightarrow M4 \longrightarrow M3 \longrightarrow M4$
$D_{on} \ge 50 $	$M1\longrightarrow M2 \longrightarrow M1 \longrightarrow M3$

图2

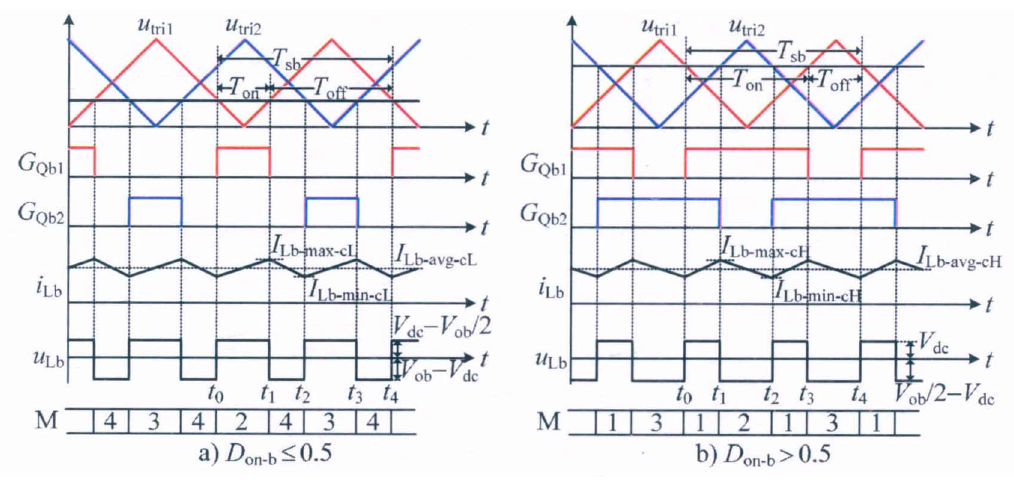
控制原理：控制占空比为三角波

在CCM下，电压增益均为$\frac{V_{out}}{V_{in}}=\frac{1}{1-D}$，可以当成一个普通的boost，但是电感可以比较小

变换器电感电流断续，即电感较小负载电阻化较大或开关周期较大时，电感DCM。因此，为保证作于CCM，需要展开分析$D_{on} \le 50$和$D_{on} \ge 50$两种情况的电感电流临界状态进行分析

1	条件$D_{on} \le 50$，若变换器工作于临界导电状态，则电感电流平均值等于电感电流增长量的一半，即$I_{avg}=\frac{I_{id}}{2}$结果式子为： $\tau =\frac{\left ( 1-D \right ) \left ( 1-2D \right ) D}{4} $ $L=\frac{V_{out}^{2}\left ( 1-D \right )^{} \left (1-2D \right )D }{4Pf} $ 这个时间常数$\tau$其实就是，固定周期下，电感与负载的一个比值，作为DCM和CCM的切换
2	在$D_{on} \ge 50$时也一样 $\tau =\frac{\left ( 1-D \right )^{2}\left ( 2D-1 \right ) }{4} $ $L=\frac{V_{out}^{2}\left ( 1-D \right )^{2} \left (2D-1 \right ) }{4Pf} $

临界电感L由输出电压、输出功率、开关频率和占空比共同决定，在变换器设计之初就应该将输出电压和开关频率确定。。开关频率的提升，可减小电感的体积。

第一步：输出电压为1800V，开关频率8KHz，
第二步：输出功率10Kw时，负载约为324Ω
第三步：输入电压为1420V，占空比为0.211
$L=\frac{1800^{2}\left ( 1-0.211 \right )^{} \left (1-20.211 \right ) 0.211}{410^4*8Khz} $ 临界电感最大为0.927mH（0.974mH）

20KW直流充电机项目

第一步：输出电压为1000V，开关频率20KHz，
第二步：输出功率20Kw时，负载约为50Ω
第三步：最低输入电压为400V，占空比为0.6
$L=\frac{1000^{2}\left ( 1-0.4 \right )^{} \left (1-20.4 \right ) 0.4}{4210^420Khz} $ 临界电感最大为0.03mH（0.03mH）

要小于临界电阻，原因如下。

电感上的能量$E=\frac{1}{2}L \bigtriangleup I^{2}$

而”$\bigtriangleup I= \frac{U *\bigtriangleup t }{L}$”

带入即可：

$E$正比于$\frac{U^{2}}{L}$可知L越小储存的能量越多