1 定性分析:
如图1为超级电容放电电路
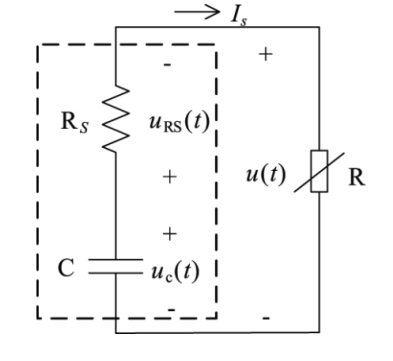
如图1所示此时公式为
$\begin{cases} & \text{ } R+ R_{S}=U_{c}(t) \\ & \text{ } I=c \frac{dU_{c}}{dt}\end{cases}$
此时初始时刻的状态为
$C\frac{dU_{c}}{dt}(R+ R_{S})=U_{c}(0)$
电容外部电压等于电容自身电压(基尔霍夫电压定律)
2 定量部分:
如图2为超级电容放电电路

电路中电流关系如下所示:
| 初始状态 | $\begin{cases} & \text{ } R+ R_{S}-U_{c}(t)=0 \\ & \text{ } I=c \frac{dU_{c}}{dt}\end{cases}$ |
|---|---|
| 进一步整理可得 | $\begin{cases} & \text{ } \frac{1}{C}\int Idt=U_{初始}+U_{C}(t) \\ & \text{ } R+ R_{S}-\frac{1}{C}\int Idt = 0\end{cases}$ |
进一步假设:设$U_{初始}=3.0V$
| $U_{初始}=3.0V $ | $\begin{cases} & \text{ } \frac{1}{C}\int Idt=3V+U_{C}(t) \\ & \text{ } IR+ IR_{S}-(3-\frac{1}{C}\int Idt) = 0=(IR+ IR_{S}+\frac{1}{C}\int Idt)-3\end{cases}$ |
|---|---|
根据高等数学齐次方程可知:电流设为$e$的对数形式($exp$形式)。将$I=e^{At+B} $带入可得上式可得:
| 将$ I=e^{At+B} $带入 | $\begin{cases} & \text{ } I= e^{At+B} \\ & \text{ } IR+ IR_{S}-(3-\frac{1}{C}\int Idt) = 0=(IR+ IR_{S}+\frac{1}{C}\int Idt)-3 \end{cases}$ |
|---|---|
| 带入收得到 | $e^{At+B}(R+R_{s})+\frac{1}{C}\int e^{At+B} dt =3$ |
| 移项 | $\\ e^{At+B}(R+R_{s}) =3-\frac{1}{C}\int e^{At+B} dt$ |
| 两边求导 | $A \times e^{At+B}(R+R_{s}) =-\frac{1}{C}\int e^{At+B} dt$ |
| 消除同类项 | $A \times (R+R_{s}) =-\frac{1}{C}$ |
最终可得
| $A= -\frac{1}{C(R+R_{S})}$ |
|---|
可知放电电流为
| 电容电流与时间的关系 | $I=e^{-\frac{1}{C(R+R_{S})}t+B}$ |
|---|---|
可知外阻影响着放电电流的衰减速率.
3 结论
结论:对于一个超级电容来说电荷量$Q$是固定的,而Q=电流X时间等价于$Q=I \times t$。故电流衰减速率越大则放电时间越短,放电时间越短则初始最大放电电流越大。
一句话结论,电阻越小,最大放电电流越大。
电流衰减速率越大则放电时间越短,放电时间越短则初始最大放电电流越大。